Objectives¶

First, the objectives can be classified in two categories:

input minimization: pack/cut all items using as few space as possible
output maximization: pack/cut as many items as possible inside all the provided containers

There is a single output maximization objective called knapsack.

For input minimization, there are 3 objective types:

Open-dimension: there is a single bin and the objective is to minimize the space used in this bin
Bin packing: there are multiple bins, the objective is to use as few bins as possible; bins must be used in the order they are provided
Variable-sized bin packing: there are multiple bins, the objective is to use as few bins as possible; there is no constraint in the order bins are used

Bin packing¶

In bin packing problems, the objective is to pack/cut all items in as few bins as possible. Bins must be used in the order they are provided.

PackingSolver supports two variants of this type of objective:

bin-packing: minimize the number of bins
bin-packing-with-leftovers: minimize the number of bins; and then maximize the value of the leftover of the last bin of the solution

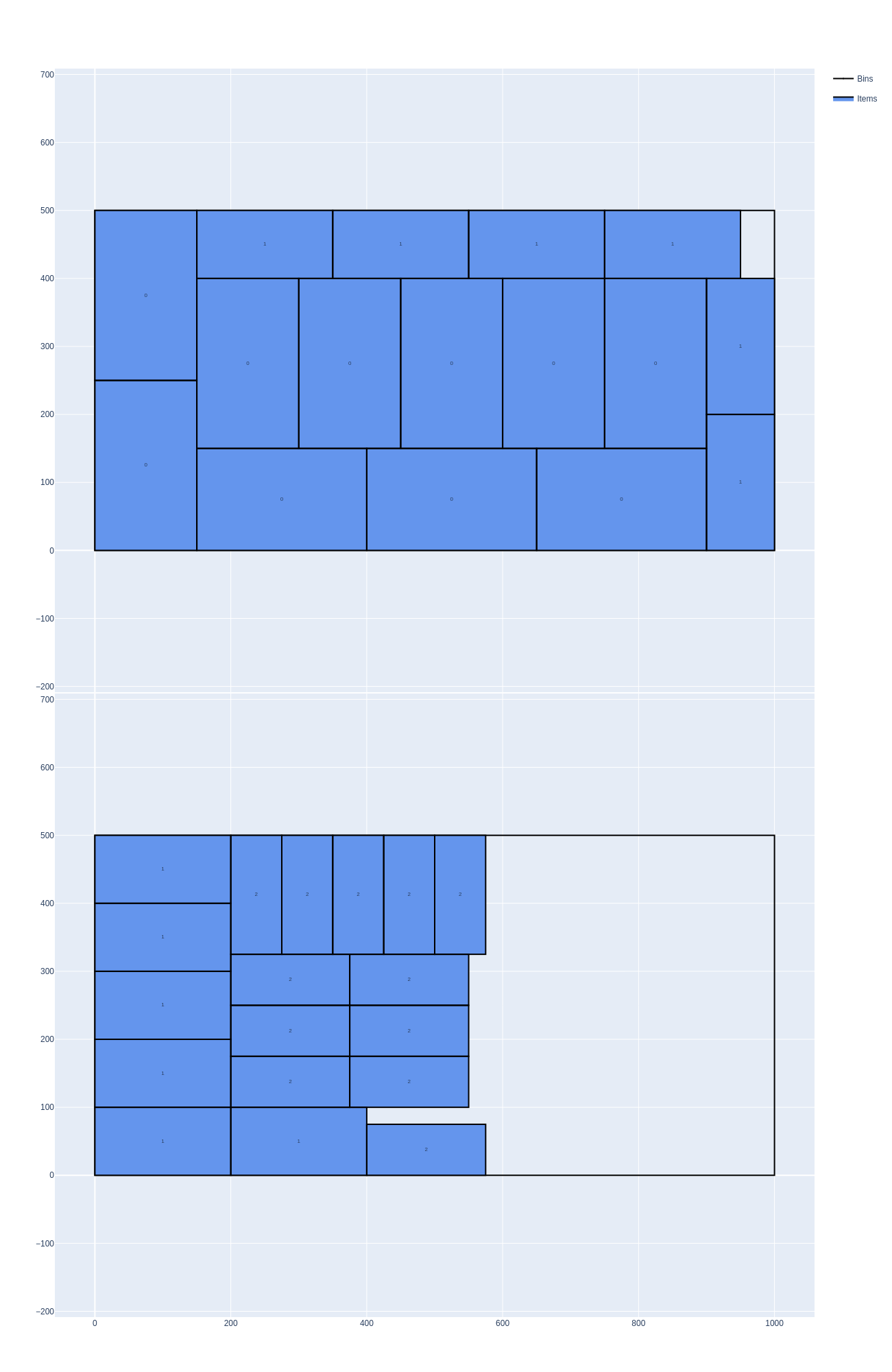
Example

In this example, there are two bin types. The first bin type has 10 copies. To use bins of the second bin type, the solution should already contain the first 10 copies of the first bin type. The solver only needs to use 2 copies of the first bin type to pack all items. Therefore, only the first bin type is used. Since the objective is bin packing with leftovers, the solver optmizes the leftover of the last bin of the solution.

items.csv¶

WIDTH,HEIGHT,COPIES
250,150,10
200,100,12
175,75,12

bins.csv¶

WIDTH,HEIGHT,COPIES
1000,500,10
700,400,10

parameters.csv¶

NAME,VALUE
objective,bin-packing-with-leftovers

packingsolver_rectangle \
        --items items.csv \
        --bins bins.csv \
        --parameters parameters.csv \
        --certificate solution_rectangle.csv

python3 scripts/visualize_rectangle.py solution_rectangle.csv

_images/objective_bin_packing_with_leftovers_solution.png

Variable-sized bin packing¶

In bin packing problems, the objective is to pack/cut all items in the cheapest bins as possible. there is no constraint in the order bins are used

Each bin has an associated cost. If no cost is provided, then the cost of a bin is its space (length, area, volume).

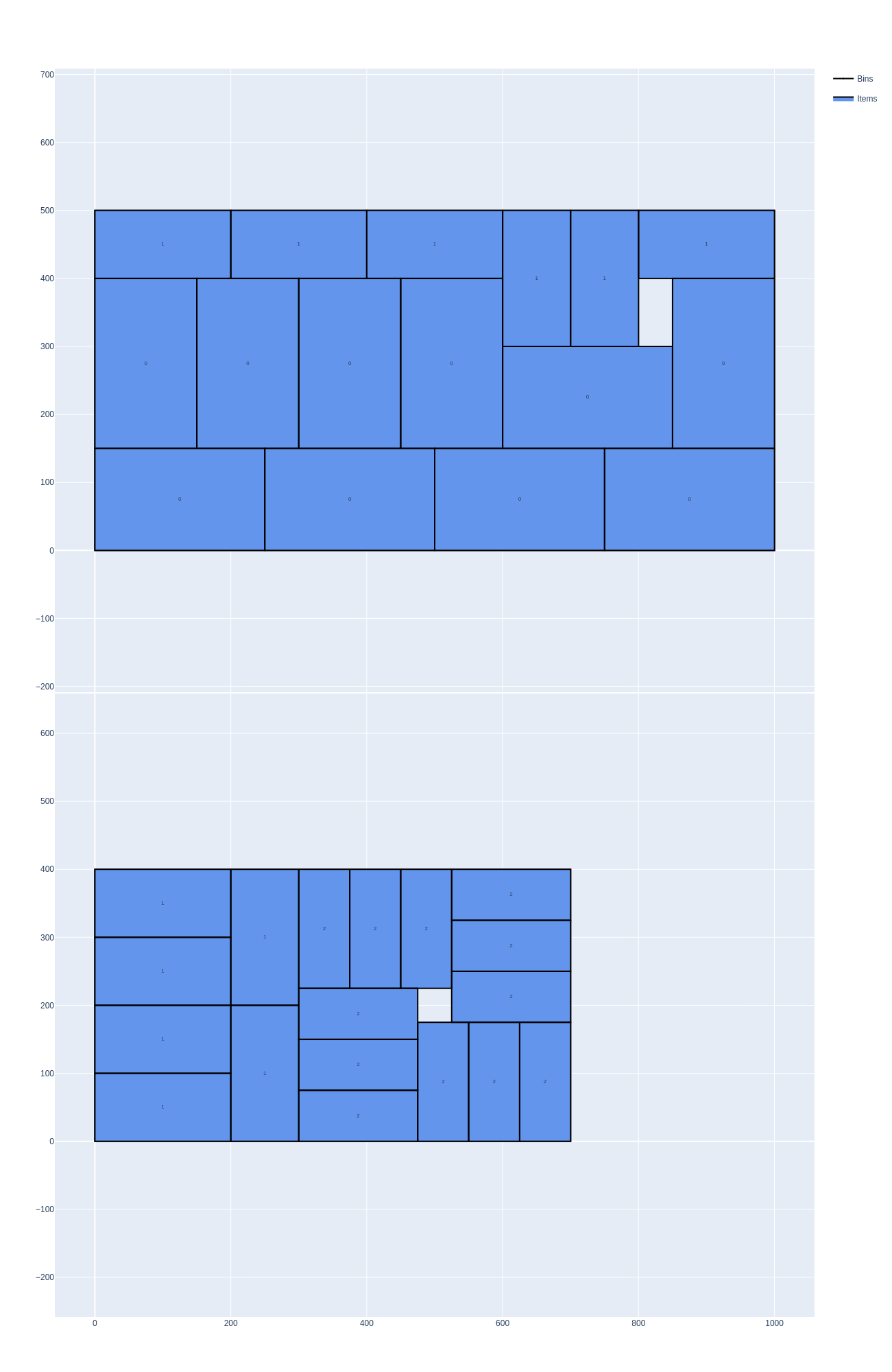
Example

The input is the same as the previous one. With the variable-sized bin packing objective, the solver can use the second bin type to minimize the overall waste.

items.csv¶

WIDTH,HEIGHT,COPIES
250,150,10
200,100,12
175,75,12

bins.csv¶

WIDTH,HEIGHT,COPIES
1000,500,10
700,400,10

parameters.csv¶

NAME,VALUE
objective,variable-sized-bin-packing

packingsolver_rectangle \
        --items items.csv \
        --bins bins.csv \
        --parameters parameters.csv \
        --certificate solution_rectangle.csv

python3 scripts/visualize_rectangle.py solution_rectangle.csv

_images/objective_variable_sized_bin_packing_solution.png

Open-dimension¶

In open-dimension problems, the objective is to pack/cut all items in a single bin using as few space as possible on the bin. As few space as possible may for example mean:

minimize the width used
minimize the height used
minimize the rectangular area used
minimize the circular area used

PackingSolver currently supports the objectives:

open-dimension-x minimize the width used
open-dimension-y minimize the height used

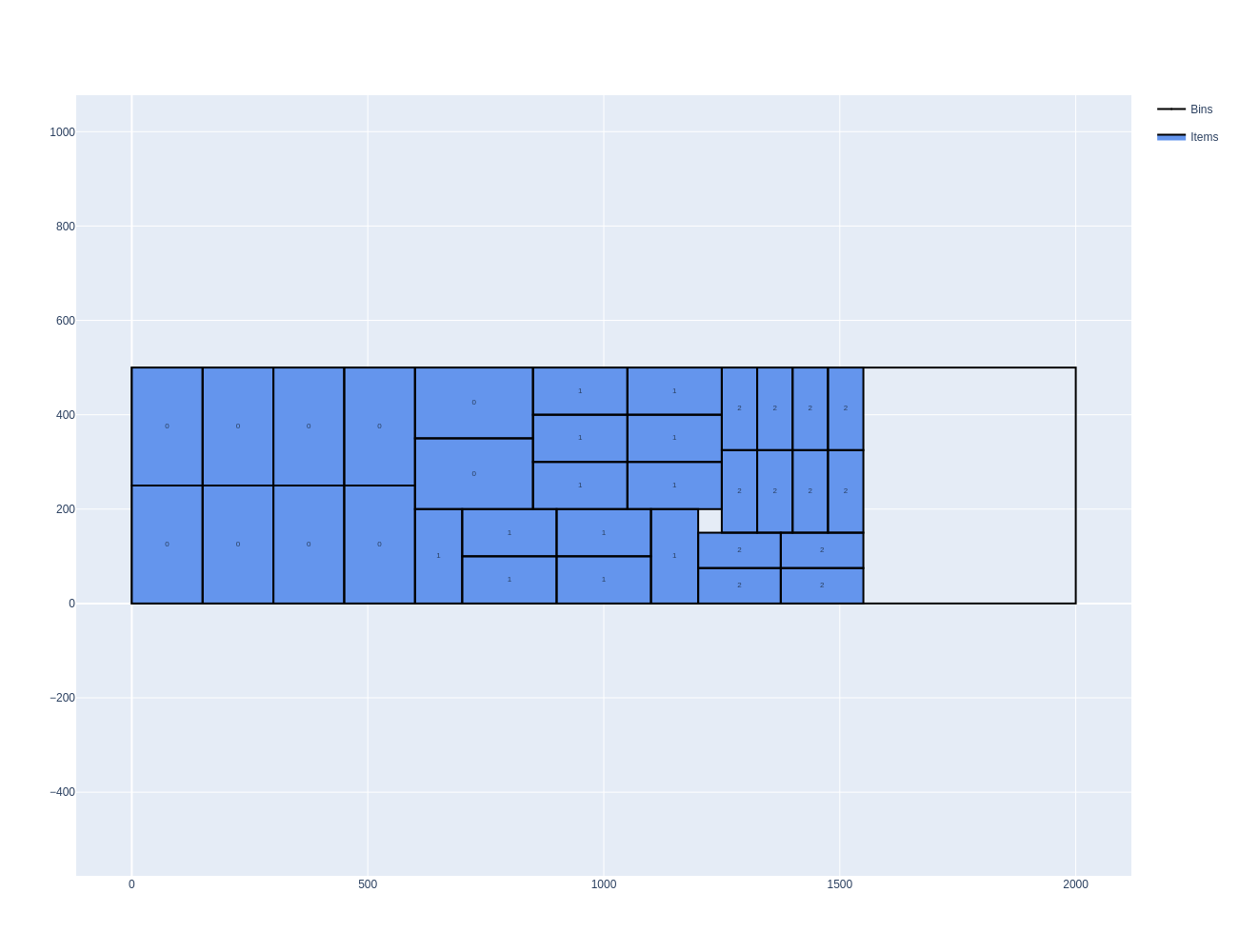
Example

items.csv¶

WIDTH,HEIGHT,COPIES
250,150,10
200,100,12
175,75,12

bins.csv¶

WIDTH,HEIGHT,COPIES
2000,500,1

parameters.csv¶

NAME,VALUE
objective,open-dimension-x

packingsolver_rectangle \
        --items items.csv \
        --bins bins.csv \
        --parameters parameters.csv \
        --certificate solution_rectangle.csv

python3 scripts/visualize_rectangle.py solution_rectangle.csv

_images/objective_open_dimension_x_solution.png

Knapsack¶

In knapsack problems, the objective is to maximize the value of the items packed/cut inside all the provided containers.

Each item has an associated profit. If no profit is provided, then the profit of an item is its space (length, area, volume).

Example

The items are the same as in the previous examples. Only 2 copies of the small bin type are available. This is not enough to pack all the items.

items.csv¶

WIDTH,HEIGHT,COPIES
250,150,10
200,100,12
175,75,12

bins.csv¶

WIDTH,HEIGHT,COPIES
700,400,2

parameters.csv¶

NAME,VALUE
objective,knapsack

packingsolver_rectangle \
        --items items.csv \
        --bins bins.csv \
        --parameters parameters.csv \
        --certificate solution_rectangle.csv

python3 scripts/visualize_rectangle.py solution_rectangle.csv